洛南中学の入試問題を解いてみた
こちらのブログでは久しぶりです。興心です。何か話題がないとこちらではブログを書いていませんが、今日は少し話題があったので書いてみたいと思います。
少し前の新聞に1/15に行われた洛南中学の入試の算数の問題が載っていたので、今時の小学生に求められている算数の力について知っておくために一部解いてみました。なかなか手強い問題が並んでいて実際に受けるのでなければ楽しい問題のセットになっています。そこまで知識が必要とされていないので、大人の頭の体操にちょうど良いかもしれません。今回はその一部を紹介しながら、解いて楽しもうというブログになります。
まずは大問1の(1)からいきましょう。こちらを簡単にしようという問題です。
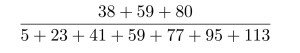
最初の問題なので計算すれば簡単に答えが求まりますが、工夫をすればもっと簡単です。こういった問題については注意深く法則が存在しないかを見てみると仕組みが見えてきます。分母を見てみると5から始まり、その後18ずつ増えていっています。また分子も同様に38から始まり、21ずつ増えています。こういったものを高校数学では等差数列とよびますが、その和は最初と最後を足したものに個数をかけて2で割ると求まることが知られています。結果として計算してみると、118で約分できるので簡単な形になります。
![]()
他にも大問1では中学数学で出てくる分配法則や方程式、因数分解(素因数分解?)を題材にしている問題が並んでおり、中学数学を勉強しておくと処理が簡単になるものが多い印象でした(大問1の(4)で452=2025であることを初めて知りました)。

ウォームアップが終わったところで、もう一問やってみましょう。大問5です。この問題はチューターや高校生にも解かせてみましたが、すんなり解いた人はおらず(というよりも誰も解けなかった…)、なかなかに難問でした。問題自体は非常にシンプルで、色の塗り分けが何通りできるかといった問題です。それでは問題を見てみましょう。
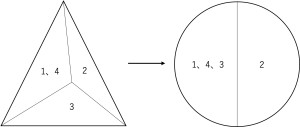
図形を形の異なるいくつかの部分に分け、赤、青、緑の3色で塗り分けます。隣り合う部分は異なる色で塗るものとし、3色すべてを使わなくても良いものとします。次の図において色の塗り分け方はそれぞれ何通りありますか。
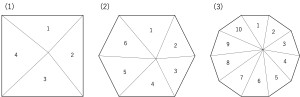
小問の流れから十角形の場合を考えるためには四角形や六角形において法則を掴む必要があります。四角形の場合は数え上げれば十分に可能な範囲ですが、それを十角形に応用できないと(3)が解けないことになるわけです。つまり実質的に法則性を見抜こうという話であり、それはなかなか簡単ではありません。
悩んだ結果、発見できた方法について共有しておきたいと思います。まずは四角形から法則を探してみます。四角形はいろいろな方法で求めることができますが、その一例について書いておきます。
まず、2色のみを使用して塗りつぶすとき、赤と青を使用するならば図のような2パターンが考えられます。色の選び方は(赤、青)、(赤、緑)、(青、緑)の3種類あるので2×3=6通りの塗り方があることがわかります。
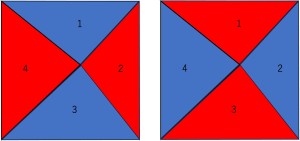
次に3色すべてを使用して塗りつぶす場合、(1、3)か(2、4)は同じ色で塗る必要があり、(1、3)を同じ色で塗った場合は2と4を使用していない残りの2色で塗ればよく、その塗り方は2通り考えられます。例えば(1、3)を赤色で塗った場合、(2、4)=(青、緑)、(緑、青)の2通りがあるということです。また(2、4)を同じ色で塗ったときも同様のことが言え、同じ色を塗るところには3色の中から1色選べるので、3色すべてを使用して塗りつぶすときは2×3×2=12通りの塗りつぶし方があることがわかります。
つまり合計18通りの塗り方があることになります。ただ、この方法は六角形や十角形には適用できそうにありません。そこで別の方法を考えてみましょう。
1から順に2、3…と塗っていくことを考えると、1には赤、青、緑の3色のどれかを塗ればよく、2には1で使用していない2色のうちどちらかを塗ればよく、3には2で使用していない2色のうちどちらかを塗ればよく、…と続いていき、四角形の場合は3×2×2×2=24通りの塗り方が考えられますが、このうちの一部は1と4が同じ色で塗られていることになります(本来は18通りであるため)。例えばこの24通りの中には(1、2、3、4)=(赤、青、緑、赤)といった塗り方が含まれてしまうことになりますが、こういった塗り方は除かなければなりません。除く塗り方は4と1を塗る色が同じ場合なので、実質三角形の塗り方となります。
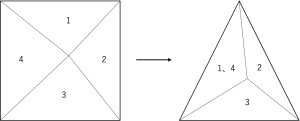
ここで三角形を1、4の場所から順に上で考えた塗りつぶし方で塗りつぶしてみると3×2×2=12通り考えられますが、やはりこの中には1、4の場所と3が同じ色で塗られたものが含まれてしまいます。これを除くためには二カ所を塗りつぶす6通りを考えればよいことになります。
結局、四角形の塗り方から三角形の塗り方を引き、その三角形の塗り方からは2箇所の塗り方を引くことになるので計算してみると24-(12-6)=18通りになります。
この方法ならば六角形や十角形にも適用できそうです。実際に計算してみると以下のように求まり答えと合致します。
![]()
今回の話はここまでですが、この計算は高校数学ではよくある等比数列の和の形になっているので、そういったところも面白い作りになっています。
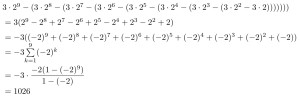
中学入試の問題を解いてみて、最近の小学生に要求されている算数の能力はなかなか高いことがわかりました。最近の小学生は大変なようです(笑)。また、問題を見ていると中学数学や場合によっては高校数学に関連するような内容のものが多く、おそらくですが中学数学や高校数学を今後理解していける力を持っているかを測りたいと思って問題を作成しているのではないかと感じました。中学入試があるような学校の場合、大抵の場合中学生のうちから高校数学を学び始めることになりますが、これは新しい分野に積極的に取り組める学生の場合、メリットが大きいシステムだと感じています。稲荷塾の場合、さらに効率的に中学数学を学ぶことにより一年で中学数学を学び終えることができるので、積極的に数学を学びたい場合はとても相性の良いシステムであると思います。中学入試を終えて今後の勉強をどうしようかと考えている場合は一度検討してみてください。
今日は中学入試を解いてみたという内容でした。
