堀川高校入試問題(数学)を解いてみた
興心によるブログの更新です。少し前に梅が咲いているのを見かけました。桜が咲くには少し早い時期ですが、春めいてきたような感じがします。ちょうど少し前に高校入試があったようですね。新聞に堀川高校や西京高校、嵯峨野高校の入試問題が掲載されていたので少し解いてみることにしました。なかなか面白い問題が並んでいますね。この前書いた洛南中学校の入試問題よりも取り組みやすい問題が多く、慣れていればかなりの高得点を狙えるような感じになっているようです。
今日は特に堀川高校の入試問題について少し取り上げてみたいと思います。誌面の都合上か、3~6番の問題しか載っていなかったので全ての問題を見たわけではないですが、ざっと見たところ、空間図形と確率、整数の問題が並んでいてオーソドックスな内容に見えます。長いブログになってしまったので興味が湧いた部分だけ読んでいただければと思います。
3番は回転体の体積を求める問題でした。小問は二つに分かれていて1つ目の小問は簡単だったので割愛します。二つ目の小問はこんな問題でした。
「図のように、1辺の長さが2である正方形ABCDがある。辺AB、BCの中点をそれぞれE、Fとする。この図形についてACを軸として1回転させたとき、四角形ABFEが通過してできる立体の体積を求めよ。」
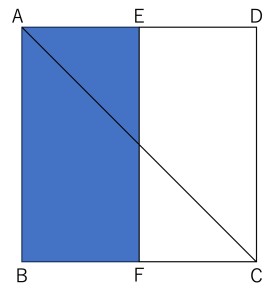
このような問題であればどのように計算しても答えは出そうですが、計算が少し簡単になる方法について考えてみることにしましょう。まずは下の図を見てみてください。S1とS2と名付けた部分は回転させた場合、完全に重なるのでS1の部分は考えなくても良くなります。
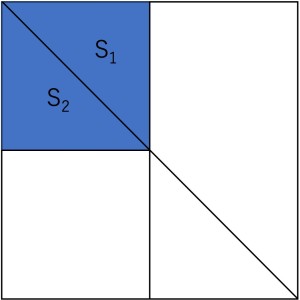
するとACの下側の部分のみを回転させれば良いことがわかりますが(下図参照)、先ほどのS2の半分の部分を矢印で示したように移動させても問題ないので、BDに対して対称な形に変形してみます。
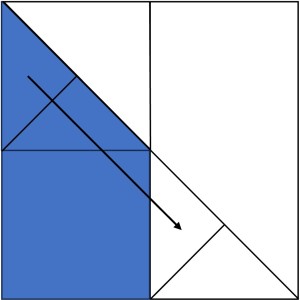
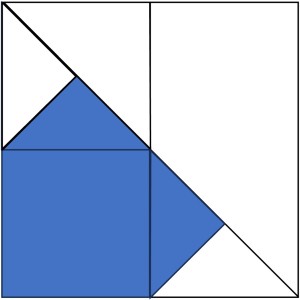
すると下図の部分を回転させた立体の体積の二倍が求める体積になります。
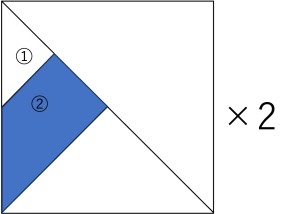
ここで上図の①の三角形と②の三角形は相似であり、その相似比は1 : 2なので、それらを回転させた体積の比は1 : 8になっており、結局②を回転させた円錐の体積の7/8が求める堆積の半分になっていることがわかります。
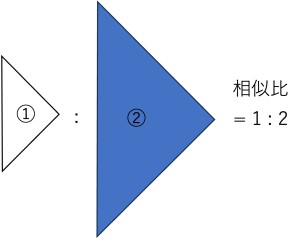
以上から②を回転させてできる円錐の底面の半径と高さがそれぞれ√2であることから体積は以下のように求めることができます。
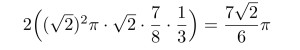
ということで3番は比較的簡単な問題でした。4番も3番と同じ空間図形の問題ですが、小問の2つ目が誘導(正四面体の全ての辺に接するということは立方体の面に接するということ)に気が付けば非常に容易なので説明を割愛したいと思います。逆に1つ目の小問は有名な話で、塾では演習数IIIの演習問題に関連した問題が出てきます(下図でDFを軸に立方体を回転させた時の体積を求める問題でした)。問題を見てみましょう。
「図のように、立方体ABCD-EFGHの各面の対角線を一辺とする正四面体BDEGがある。この正四面体の高さが2√6/3のとき、立方体の一辺の長さを求めよ。」
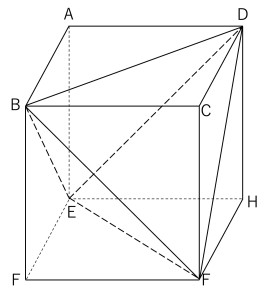
先ほど有名な話と関連していると書きましたが、どういった話かについて説明しておきます。下図のように平面ACH、平面BEFを考えてDFとの交点をそれぞれI、Jとするとき、DI : IJ : JF = 1 : 1 : 1になるという話があります。これは数IIBまで勉強すればベクトルで簡単に説明できます(DAベクトル、DCベクトル、DHベクトルを設定してIが直線DF上の点であり平面ACH上にあることを言えばおしまいです)。
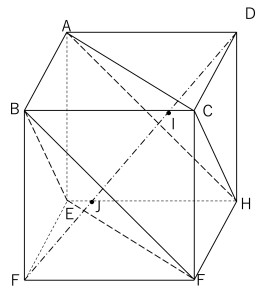
この話からDF=√6となるのでこの立方体の一辺の長さは√2になります。簡単な問題でした(笑)。ただし、話はここで終わらず、問題文の最後に「なお、解答欄には解答だけでなく、計算の過程や説明も記入しなさい」とあるので、そうなってくると少し面倒です。立方体の一辺の長さをxとでも置いて立方体の体積から出っ張った部分を取り除き正四面体の体積を計算した上で正四面体の底面(正三角形)の面積をxで表したら高さの情報からxが求まりそうですね。
5番は確率でした。高校数学的には簡単な問題ですが、中学生には独立の概念があまりないので難しいのかもしれません。問題文が長いので図を交えて問題を説明したいと思います。
「A、B、Cの三つの袋に図のように書かれたカードが2枚ずつ入っている。それぞれの袋から一枚ずつ取り出す作業を一回の試行とし、カードの数字が全て異なった場合は−1点、カードの数字のうち2枚が同じで残る1枚が異なった場合はその数字を点数とし、カードの数字が全て同じであった場合は+4点とする。最初の持ち点を2とし、二回の試行をカードを袋に戻しつつ行うとき、それぞれの確率を求めよ。
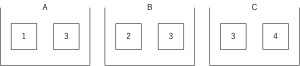
- 得点が0点になる確率
- 得点が2点となる確率
- 得点が5点以上となる確率」
まずは一回の試行でどうなるかについて考えることにしましょう。カードはそれぞれ2枚ずつ袋に入っているので取り出し方は8通りあります。A、B、Cからひいたカードに書かれた数がa、b、cであったとき、(a, b, c)と表すことにすると、−1点となるのは(1, 2, 3), (1, 2, 4), (1, 3, 4), (3, 2, 4)の4通りで起こる確率は1/2となります。+1点となるのは(1, 3, 3)となる1通りで1/8で起こり、+2点となるのは(3, 2, 3)となる1通りで1/8で起こります。+4点となるのは(3, 3, 3), (3, 3, 4)となる2通りで1/4で起こります。ここまでは8通りを書き出して注意深く確認すれば簡単にわかることです。
次に問題を解いてみましょう。二回の試行で0点となるのは−1点が二回連続して起きるときなので(1/2)×(1/2)=1/4となります。
二回の試行で2点となるのは+1点と−1点が一回ずつ起きるときなので、どちらが先に起こるかで2パターンあり、2×(1/2)×(1/8)= 1/8となります。
問題は5点以上となるときです。余事象を考えるべきか悩みますが、そのまま計算した方が早そうです。最初の持ち点が2点なので一回目に−1となると二回目は+4、一回目に+1となると二回目は+2以上、一回目に+2となると二回目は+1以上、一回目が+4となると二回目は何が出ても良くなるので結局計算としては以下のようになります。
(1/2)×(1/4)+(1/8)×(1/8+1/4)+ (1/8)×(1/8+1/8+1/4)+(1/4)×1=31/64
しかしながら小問の3番は数え損ねる場合もあるのではないかと思います。
最後の6番は整数の数え上げの問題でした。問題文は以下のようになっています。
「自然数nについて<n>を「nが2で何回割り切れるか」を表す記号とする。またxを1≦x≦100を満たす自然数とする。
(1)<x>=3を満たすxはいくつあるか。
(2)<2x2>=5を満たすxはいくつあるか。
(3)<x2+16x>=9を満たすxはいくつあるか。」
(1)についてはxが8(=23)の倍数かつ16(=24)の倍数ではない場合なので、書き出してみると、8, 24, 40, 56, 72, 88の6個です。8×12=96(<100)なので100までの自然数の中に8の倍数は12個ありますが、そのうち半分は16の倍数になっているので6個としても良いでしょう。
(2)については問題文の意味からx2が16の倍数かつ32の倍数ではない場合を言っているので、xが4の倍数かつ8の倍数ではないということになります。これも数えてみると13個となります。高校数学的にはガウス記号を用いて[100/4]−[100/8]=13とするとスッキリしますね。
(3)については少し状況について考えないといけません。高校数学では合同式(ある数で割ったときの余りの話)について学びますが、少し近いものを感じます。実際に調べてみましょう。
<x>=aであるとすると、x=2a×(2b−1)と表すことができます(ここでのbは整数です)。すると以下のようになります。
x2+16x=x(x+16)= 2a×(2b−1){2a×(2b−1)+16}
ここでa≦3のときは<2a×(2b−1)+16>≦3となるので<x2+16x>≦7となり、不適です。
逆にa≧6のとき<2a×(2b−1)+16>≧4となるので<x2+16x>≧10となり不適です。
つまりa=4, 5に限られます
a=4としてみると
x2+16x=24×(2b−1){24×(2b−1)+16}=29×(2b−1)×b
となるのでbが奇数でないとダメです。つまりx=16, 80に限られます。
a=5としてみると
x2+16x=25×(2b−1){25×(2b−1)+16}=29×(2b−1)(4b−1)
となるのでbに関係なく成立します。このときx=32, 96です。
以上よりx=16, 32, 80, 96であれば条件を満たすので4個となります。
大変面倒な問題でした。時間内に処理しきった受験生はどれくらいいたのかが気になりますね。
一通り解いてみた結果、今回の問題のセットの中で明らかな難問はありませんでした。しかしながら、解法を自分で考える癖をつけていないと本番で問題文を読んだときに手がつけられない場合も多かったのではないでしょうか。個人的には塾で中学数学の演習を行っている内容と同レベルのものが問われているように感じたので、ちょうど良い難易度だと思っています(以前書いた洛南中学の入試問題よりは手をつけやすかった笑)。
こうして入試問題を解いてみると、中学入試でも高校入試でもその後の勉強を理解していけるかどうかを測ろうとしているように感じます。基礎的な内容に絡めて少し考えないと答えに辿り着かない問題を何問か出すことでパターンを覚えているだけの受験生を判別したいという意図がありそうです。なかなかに解いていて面白い問題でした。ぜひ暇があれば他の解法についても考えてみてください!今日は堀川高校の入試問題を解いてみたという内容でした。
